デジタルハリウッド大学と現実科学ラボがお届けする「現実科学 レクチャーシリーズ」。
「現実を科学し、ゆたかにする」をテーマに、デジタルハリウッド大学大学院 藤井直敬卓越教授がホストになって各界有識者をお招きし、お話を伺うレクチャー+ディスカッションのトークイベントです。
X(旧Twitter)のハッシュタグは「#現実とは」です。ぜひ、みなさんにとっての「現実」もシェアしてください。
概要
- 開催日時:2025年1月31日(金)19:30~21:00
- 参加費用:無料
- 参加方法: Peatixページより、参加登録ください。お申込み後、Zoomの視聴用リンクをお送りいたします。
視聴専用のセミナーになりますので、お客様のカメラとマイクはオフのまま、お気軽にご参加いただけます。
ご注意事項
- 当日の内容によって、最大30分延長する可能性がございます。(ご都合の良い時間に入退出いただけます。)
- 内容は予期なく変更となる可能性がございます。
- ウェビナーの内容は録画させていただきます。
プログラム(90分)
- はじめに
- 現実科学とは:藤井直敬
- ゲストトーク:西郷甲矢人氏
- 対談:西郷甲矢人氏 × 藤井直敬
- Q&A
登壇者

西郷 甲矢人
数学者(長浜バイオ大学教授)。
1983年生まれ。博士(理学)。専門は数理物理学・非可換確率論。
『〈現実〉とは何か』(筑摩書房、田口茂氏との共著)ほか著書多数。

藤井 直敬
株式会社ハコスコ 取締役 CTO
医学博士/XRコンソーシアム代表理事
ブレインテックコンソーシアム代表理事
東北大学医学部特任教授
デジタルハリウッド大学 大学院卓越教授
MIT研究員、理化学研究所脳科学総合研究センター チームリーダーを経て、2014年株式会社ハコスコ創業。主要研究テーマは、現実科学、適応知性、社会的脳機能の解明。
共催

※本稿では、当日のトークの一部を再構成してお届けします。
20世紀の革新「相対論」と「量子論」
藤井 昨年、北海道大学の田口茂先生にご登壇いただきましたけれども、本日はその田口先生と一緒に『<現実>とは何か』という本を出しておられる西郷甲矢人先生をお招きしました。過去に数学者のゲストはいらっしゃらなかったと思います。僕は数学がすごく苦手だという自覚があるので、今日も途中で分からないことがあったら教えてください。よろしくお願いいたします。
西郷 よろしくお願いします。まず、私がどういうことを研究しているかをお話しします。ここに「量子場」というものがあります。分かりやすく言えば、例えば光なんかもそうですけど、この世のありとあらゆるものが原理的には量子場のふるまいとして理解できるだろう、と考えられているんですね。
で、この量子場とはどんなものなのか簡単に説明します。20世紀の物理学の偉大な革新に、「相対論」と「量子論」というものがあります。相対論は、いわゆるアインシュタインの相対性理論ですね。相対性理論においては、時間と空間がバラバラではなくて一体をなしているものと考えないといけないとか、そういうことを聞いたことがあろうかと思います。
量子論は、原子以下の世界、素粒子とかそういうものに関わるようなレベルの世界に行きますと、大変ふしぎに思われるようなふるまいをしていることがわかってきた。それで、こういうものを数学的にとらえて厳密な解析を行うことを求めて、量子論が生まれました。
二つの理論を統合するという未完のプロジェクト
西郷 相対論も量子論も、大学の理学部、工学部などでも習う非常に基本的なものになっていて、覆そうと思っても覆せない偉大な、重要な理論として確立されています。ところが、この重要な二つの理論、統合しようとするとなかなか難しいものなんですね。
世の中の根本的なありようは相対論にも従うべきだし、量子論にも従うべきだ。光も電子もこういうふるまいをするはずだ、というのを考えているのが量子場なんですけれども。非常に残念な、そしてある意味面白いことに、数学的な厳密さのレベルでもって相対論と量子論を十全に統合することは未だできていない。未完のプロジェクトであるということなんです。
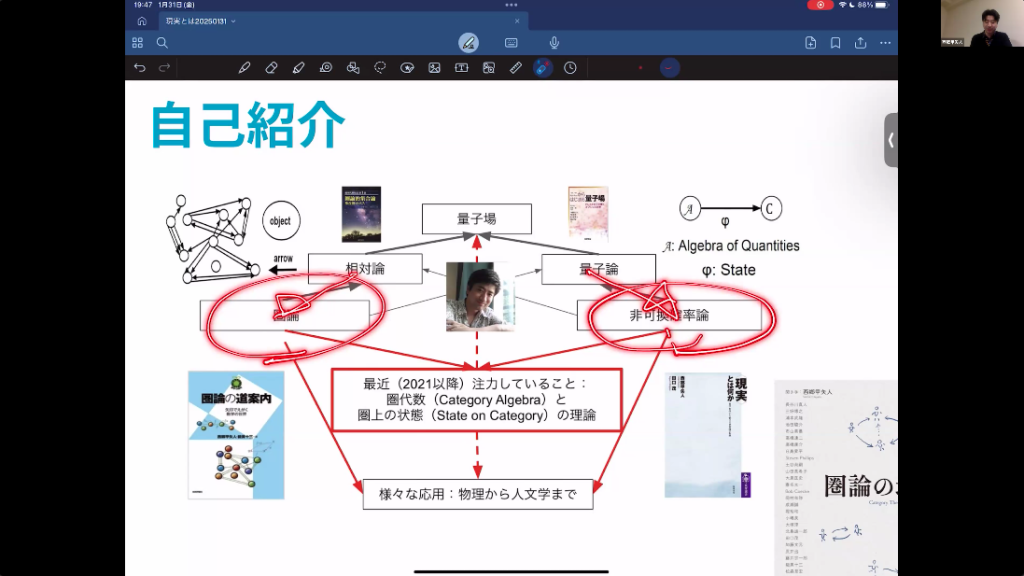
私も大変非才な者でありながら、こういう大問題に取り組もうと思ってやってきました。皆と同じ道を行っても太刀打ちできませんから、ほとんど望み薄のようなところから、数学者らしい回り道をしてみたいと思ったわけです。
二つのものを統合しようとする時、我々数学者はもっと難しい問題を考えようとします。これとこれをくっつけるなら、これをもっと一般化したもの。相対論をもっともっと一般化した何かと、量子論をもっともっと一般化した何かを考えて、そのレベルでつなげられないかと。こういう絶望的なことを考えるようになったわけです。
私の見立てでは、相対論を一般化したものとして理解できるのが「圏論」。量子論を一般化した「非可換確率論」、これは数学の理論として私の専門でもあります。これをつないでいくことで、いつか量子場に行きたいと考えていました。非常に拙いものではありますが、この二つをつなぐ数学の理論も出来始めていて、大変楽しく過ごしているところです。
現実が孕む「不定性」
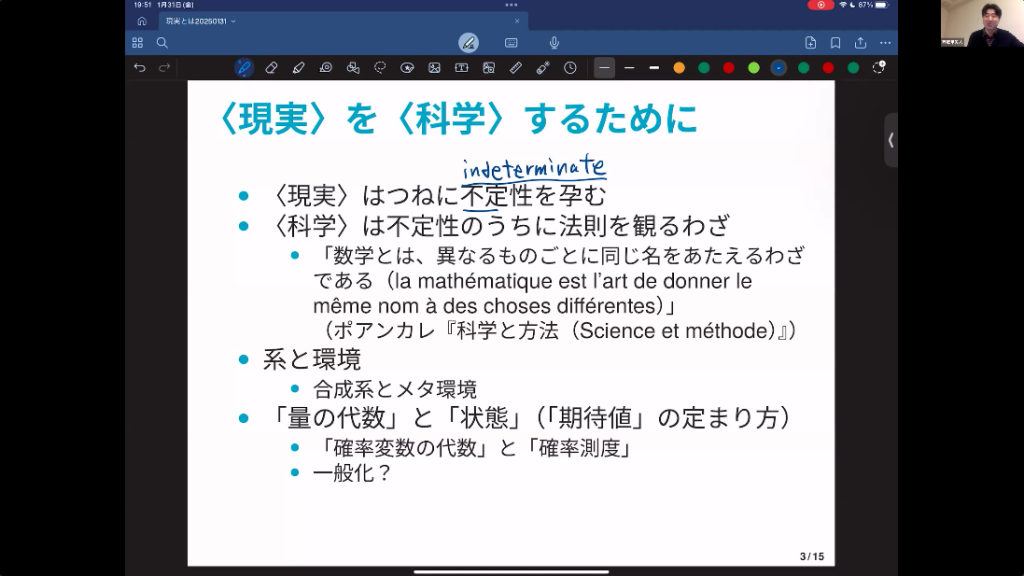
西郷 それで、「現実科学」ということで。「現実」と「科学」、この二つの言葉をしっかり見ていく必要があると思います。「現実」について私が強調したいのは、不定性を孕んでいるという点です。つまり、定まっていないということなんですね。
分かりやすく言うと、全ては見えていないということです。私は今、パソコンを見ているけど、その裏側は見えない。月の裏側も見えない。私たちは全てが明らかに目の前にあるというふうには現実を経験していなくて、何か予想外のものが現れてくるんじゃないかっていう期待や不安、そういうものを常に持っているはずです。
そして面白いことに、以前は我々に見えないだけで、月の裏側にはもうハッキリと確定された何かがあるだろうと思う余地がまだあったんです。でも量子論により、単に我々が知らないだけではなく、本当にこの現実の中に定まっていないような、不定なありようがとても大切なものとしてあるんだ、ということが分かってきました。
未来も、決して最初から決まっているわけではなくて、自らも主体としてどんどん変革していくことができるものとしてある。そういう意味で、確定されたものではなく、不確定なところを持っている。常にそういうものを孕んでいるのが現実である、と言えると思います。
不定性に満ちた現実に法則を観る
西郷 一方、科学ですね。これは、不定性に満ちあふれたこの現実に、一種の法則性を観る、そういうアートである、と言うことができると思います。アートとは、技術であり、芸術であり、「わざ」です。
何が起きるか分からないけれども、少なくともこの部屋でペットボトルが何もしないのに空中にふーっと浮き上がることはないだろう、とかね。手を離せば落ちるよねとか、そういうような法則性ですね。これは別に大人の科学者だけがしているわけではなく、赤ん坊から死ぬ間際の人まで、誰しもがやり続けていて、またそれを面白いと思っている。人間性とは、不定性の内に法則を観るのが楽しいという、そういうものでもあると思います。
藤井 不定であるが故にどうなるか分からないとしたら、法則も未来永劫同じではないということですか?
西郷 そう思います。ただ、ほとんど変化しないような法則、例えばエネルギー保存の法則のような、何回も疑われながら何回も確かめられて安定しているものもあります。でも、それにしてもより一般化されないといけなかったり、明日には変わったりするかもしれない。まして人間に関わる様々な法則というのは、どんどん変わっていくし、変わっていくべきものだと思います。

法則はつきつめると数学に行き着く
藤井 検証は常に行わないと、不定性があるかぎりどこかで変わってしまう可能性がある。
西郷 その通りだと思います。我々は広い意味でみんな科学者なんですが、数学に縁がないとか苦手だと思う人であっても、何か徹底的に法則性みたいなものを考えていこうとすると、どうしても数学になっちゃう、あるいは数学と関わりを持ってしまう。それこそ、そういう法則性が科学にはあるように思います。
偉大な数学者ボアンカレが「数学とは、異なるものごとに同じ名をあたえるわざである」と言っているんですね。法則とは、ある種の再現可能性です。でも、厳密にはどんな現象も二度と繰り返すことはない、異なるものごとなんですよね。
でも、その異なるものごとに同じ名を与えることが必要になる。その同じ名って何なの?と考えると、例えば構造であると。じゃあ、構造が同じってどういうこと?と徹底していくと、嫌でも数学的構造という問題に入ってしまう。
「系」と「環境」の相互関係
西郷 いよいよ、私の専門である非可換確率論の話に入っていきます。現実の中で現象は刻々と変化していくわけですが、法則性を見出そうと思ったら、現象を切り出してくる必要があります。
物理学をはじめ、サイエンスの世界では「系」(システム)という言葉を使います。この世界の一部をなしている、ある種の同一性を考えられる一部を系と呼ぶんですね。例えば、このペットボトルもそうですし、細胞、社会もそうかもしれない。で、それに対してどういうことが起こり得て、どういうことが起こり得ないのかを考えていくわけですけれど、そのためには「環境」というものを考える必要があります。
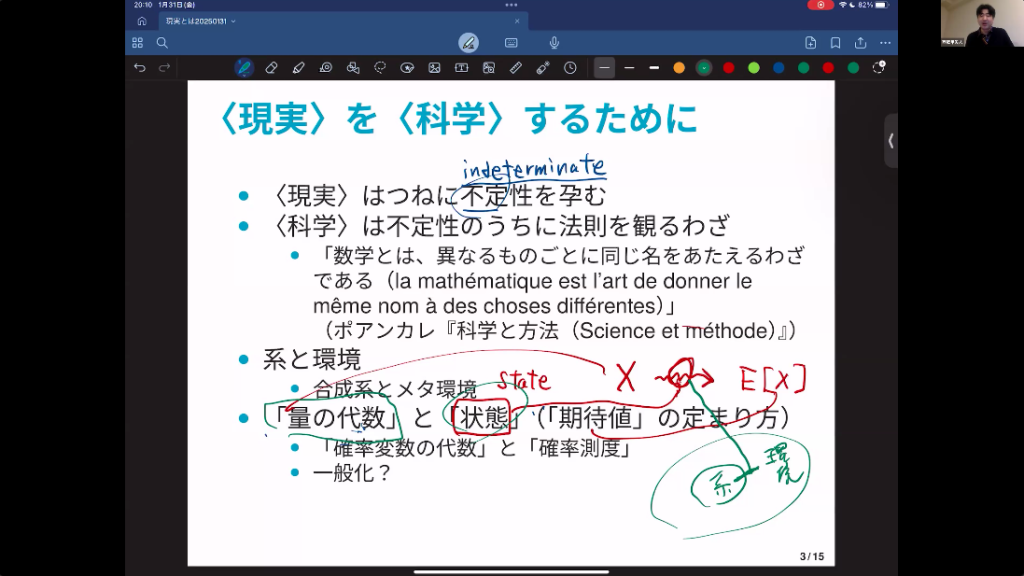
私が今、このペットボトルから手を離したら誰もが「落ちる」と思います。だけど、それは私が地球上のこの部屋にいるからなんですね。例えば、これが宇宙船の中なら全然違うことになります。系に起こりうるものごとは、それと密接に関係する系、いわゆる環境との関係性の中で、初めて色々なふるまいをするということなんですね。この相互関係を考えていく必要があります。
どこまでを系とみなすかは、人間が結構自由に選ぶことができます。選んだものについてどんな風なことが成り立つかは勝手に選べませんが、そういう意味での自由さというのもあるわけです。
性質を量という側面から考える「代数」
西郷 いよいよ数学になってきます。我々がこの系について何か語りたいと思う時に、例えばペットボトルから水を飲んで「うまいなあ」とか「味がないなあ」とか、色々な経験をすることができる。でも、実際に飲んでいない人に共有するのは難しいですね。そこで、例えば水のミネラルの濃度を測ってみるとか、温度を測ってみるというふうに数値化すると、シェアしやすい形になります。
システムの様々な性質を量という側面で切り取ってみる。で、例えば温度ならこれも熱くなったり冷たくなったり、環境との相互作用の中で揺らいでいます。揺らぎの平均とか、分散、様々な量について、足し算とか掛け算とか、何とか算で扱うことができる特性を考える。これを、我々は「代数」と呼んでいるわけです。
量子論の中にいくと、本当に値自体が決まっていないような状況も出てくる、まさに不定なんですが、大体の傾向は語れることがあるんですね。この期待値を考えることが大事です。
「状態」はシステムの量と期待値の対応づけの法則
西郷 で、今日覚えて帰っていただきたいのは「状態」(state)という言葉です。例えば、温度という量に対して、その平均値、期待値を対応させる。その対応づけのルール、法則性のことを状態と言います。これを覚えれば、もう量子論のエッセンスをつかんだと言っていただいても大丈夫です。
水の例えでいえば、温度は系だけで決まるわけではなくて、どんな環境に置くかによって決まります。この系と環境の相互作用のあり方が、実は状態です。別に数学や物理興味ないやっていう方もね、「意識の状態」とか、「社会の状態」という言葉を使うじゃないですか。状態って、実はものの中にあるんじゃなくて、ものと他のものとの関係性のなかにあるんじゃないか、ということです。

藤井 一般に僕らが使う「状態」っていう言葉と、西郷先生がおっしゃった「状態」は違うという理解ですか?
西郷 一見違うように感じると思うんですが、我々が何かの「状態」と言っているものって、このルールを定めることに他ならないと思っていて。そのルールは系だけで決まるのではなく、環境との相互関係で決まるんだというのは、私の知る限りは量子論に限らずどこでもそうなっていると思います。
藤井 なるほど。じゃあ、あんまり難しく考えなくてもいい?
西郷 そうそう。「私の心の状態」って何だろうと考える時に、本当に私の中だけで決まるんでしょうか?っていう。そんなことないですよね、って考えてみれば、決して奇抜なことを言っているわけではないと分かっていただけると思います。
決定論からの根本的な離脱
西郷 それで、量の代数とか状態って具体的にどんな話なんですか?というと、確率論で確率変数という言葉があります。要するに、偶然的に揺らぐ量のことです。例えば、明日の降水量とかね。降るかもしれないし、降らないかもしれない、その確率の重みだけが決まっている。それは充分な情報がないから分からないだけだろう、とイメージする人も多いでしょう。ところが、量子論というのは、その現実に対する考え方を覆すようなものです。
非常に簡単に言いますと、量子論は決定論からの根本的な離脱を我々に強いた。ここでいう決定論はめちゃくちゃ簡単で、Aが起こったら100%の確率でBが起こる、みたいなことです。これがずーっと連なっている。Aが起こったらBが起こって、Bが起こったらCが起こって、と宇宙開闢以来、完全に運命のように展開していくんだ、というのが物理学者にはあったんですよ。確率を考えないといけないのは我々の無知のせいだ、と。
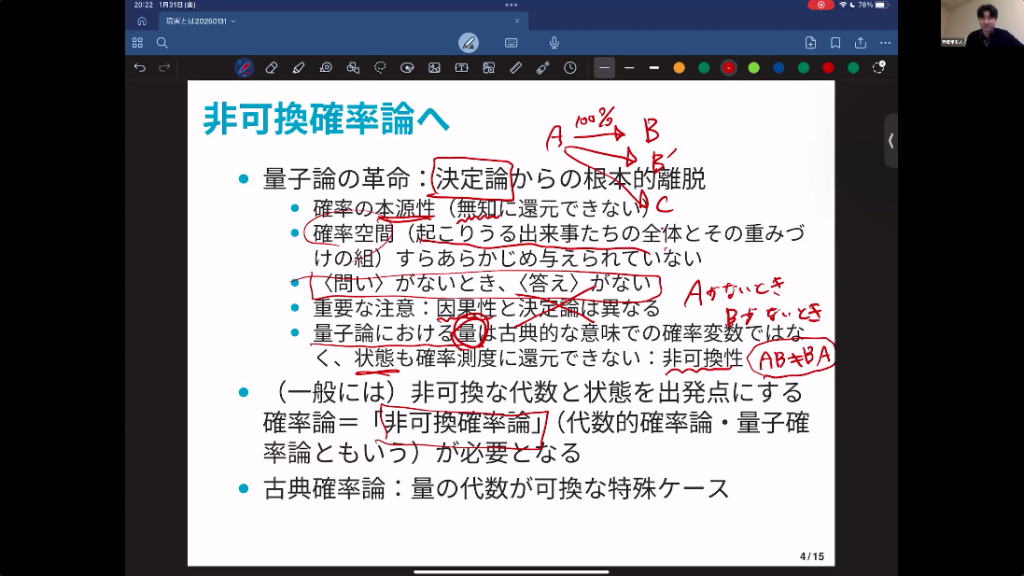
量子論に至ると、さすがにそれは捨てなきゃいけないということが分かってきた。Bに行くかもしれないし、B’やC’に行くかもしれない。そういう可能性を秘めていることを認めざるを得ない。我々が知らないだけで値は確定しているとか、そういう解釈がどこかしらで破れることを量子論は教えてくれたわけです。
<問い>がないとき、<答え>がない
西郷 キャッチフレーズで言うと「<問い>がないとき、<答え>がない」という構造です。例えば、ある電子の位置を測りたいと思ったとします。そうすると、位置については確率分布が決まる。でもその時、運動量については想定すらできない。運動量を測ろうと頑張ると、運動量も決まります。でも、その時は位置が全然決まりません。
問うたら答えは出てくるんだけど、問う前に答えはない。現実というものの一番基礎、根本にあるレベルでそういうことが起こっている。決定論が成り立たないどころか、その大前提が破られてしまう。
系と環境という言葉でいうと、我々は何かを測定しようとするときに、測定装置とそれを相互作用させないといけないですよね。だから、我々は問いかけという形でシステムにカップルしていく。やり方を決めて、初めて何かが確定し得るという構造があるんです。
注意して欲しいのは、因果性がそれで否定されたわけではないということです。「Aがないとき、Bがない」といったタイプのルールは、破れていません。無から有が生じるとか、種も蒔かないのに芽が生えるみたいな、そんな何でもありなことが量子世界で起こっているわけではありません。
プロセス的なものはABとBAがいつも同じとは限らない
西郷 では、こういう問いがないとき答えがないみたいなタイプの確率性をどう数学にできるんでしょうか?これは、古典的な意味での確率変数ではない。どういうことかというと、数値以上のものなんですね、量っていうのは。それはある種の働きのようなもの。問いかけに対する答え、レスポンスのようにもっと動的でダイナミックなもの、操作的なものに近いということが分かってきた。
操作っていうのは、ABとBAがいつも同じとは限らない、という世界ですね。数値であれば、2×3と3×2は同じなんですよ。掛け算の順序なんか関係ない。ところが、お湯を沸かしてから味噌を入れるか、味噌を入れてからお湯を沸かすかで味噌汁の味が変わるように、操作は順番を入れ替えたらややこしいことになってくるわけです。
量というものすら、プロセス的なもので非可換であることが分かってきた。それを含む世界はより一般化された確率論が必要で、それが実は非可換確率論で、これが私の専門分野です。
非可換確率論の応用
西郷 よく「量子物理学の時だけ非可換確率論を用いるんですか?」と勘違いされますが、実際はそうじゃないんですね。興味深い応用例として、非可換確率論を用いて人間の認知をモデル化しようという話があります。
昔からよく知られている話で、質問の順番を変えて聞くと結果がだいぶ変わるっていう現象があるんですよね。Aですか?って聞いてからBですか?って聞く結果の分布と、Bですか?って聞いてからAですか?って聞く結果の分布がずれてくるのはよくあることです。
このようなちょっと説明しにくい人間の認知の現象を体系的に説明するのに、驚くべきことに量子現象の解析をするために作られた数学が役立つということが知られています。ですから、非可換確率論って、色んなところに応用可能なんですね。
プロセスの集まりの全体、「圏」
西郷 実は物理に限らず、「圏」(category)という数学的構造を持っている現象に中にある場合には、自然にこの非可換確率構造が現れてくるということが、不肖私によって発見されました。圏というのは、直感的にいうとプロセス、過程の集まりみたいなものを、数学的に厳密に定式化したものだとイメージしてもらえればいいかと思います。
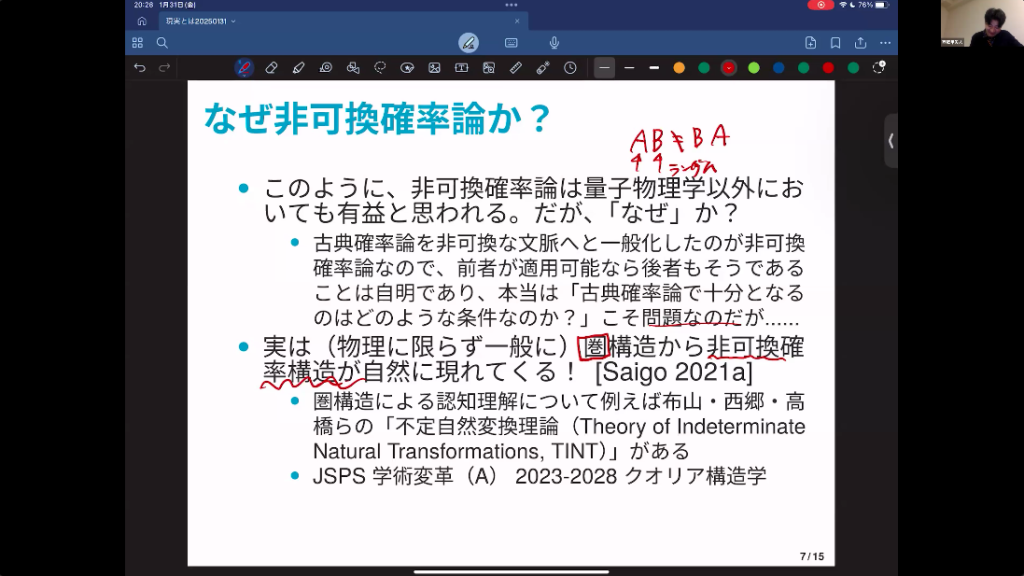
過程って何となく矢印で書くじゃないですか。出どころがあって、行き先がある。この矢印みたいなものを、我々は「射」と言っています。で、この出どころと行き先にあたるポイントを「対象」と呼びます。で、始まりと終わりを共有しているような2つの矢印があると、「合成」といって、その結合律について簡単な法則が成り立っている。またこれも重要なんですが、何もしないというのも一つのプロセスです。こういうルールを持つものを「圏」と言います。
具体例では、プログラムって何かの型のデータを別の型のデータに変えることですね。入れるデータの型と出ていくデータの型っていう始まりと終わりがあるし、プログラムをガッチャンコさせるとまたプログラムになりますね。他に何でもあります。要するに、人間がプロセスの総体のことを考えると、これは圏ということになります。
藤井 始まりと終わりの点は何でもいいんですか?
西郷 ルールさえ満たせば何でもいい。あらゆる可能なプログラム、みたいなものも圏をなしていますし、私の手がどう動くことが可能か、みたいなことも圏をなすんですね。こういう動きをした後はこういう動きができるし、とか可能な運動の全体みたいなもの。大体人間がプロセスの集まりだと思うものは圏になっている。
矢印の足し算・掛け算を可能にする「圏代数」
藤井 ここから非可換確率論がどうつながってくるのか、よく分かりません。
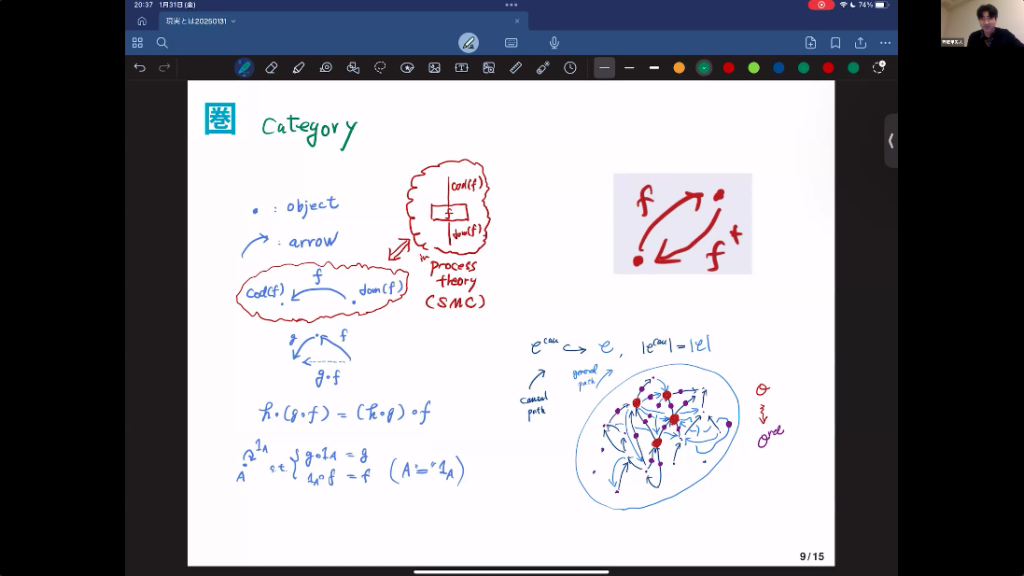
西郷 で、圏から「圏代数」というもの作ろうと思うんです。代数というのは、さっきの足し算や掛け算ができるようなものですね。具体例で言うと、鉄道網というのがあります。色々な路線があって、可能な交通を射だと思えば、まさに「交通圏」があるわけですね。
電車や交通は矢印の集まりみたいな格好をしている。そこで、○○電車と△△電車だけで行けるところはどこでしょう?のような問題を考えてみる。矢印をつなげて、つながらないのは消して、つながるのだけ残して、みたいな。こうすると、自然と矢印の集まりの掛け算みたいなものを定義できると、まあそんな発想なんです。
中学高校の初心に返っていただいて、最初にXとかYとかの文字式を習った時にすごく大変だったと思うんですけど。この文字のことを数学では不定限と言います。要するに、どんな値をとるか決まっていないものを、文字として考えます。それを混ぜ合わせると式ができるわけですね。
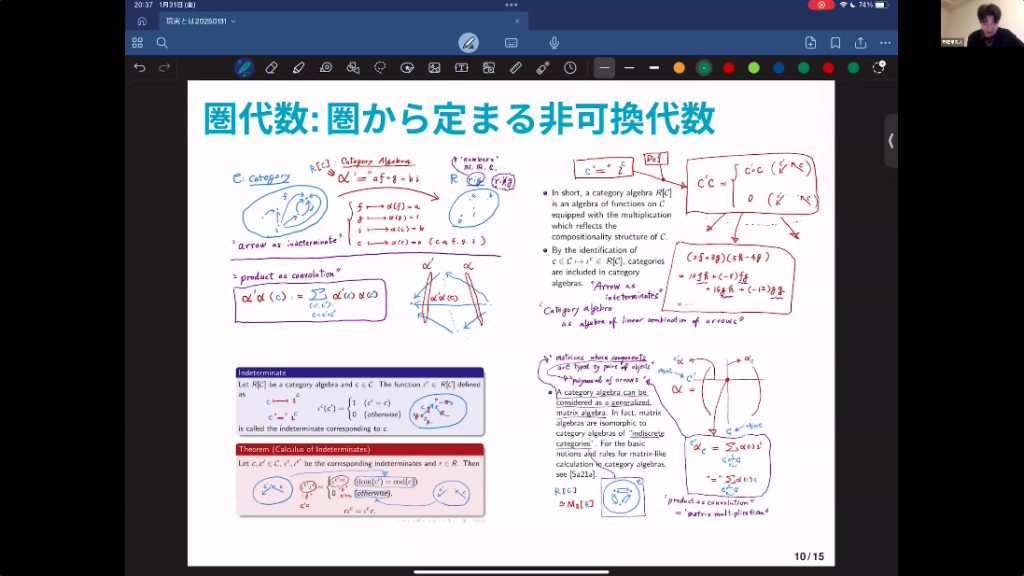
で、このプロセス、矢印ひとつひとつを文字みたいなものと思って、その文字から作られる文字式みたいなものを考えるよと。そういうことをしているのが圏代数です。矢印がちゃんとつながっていれば、合成を掛け算と思ってくださいと。つながってなければ0とする。そうすると、普通に計算ができるようになりました。普通の文字式の計算とひとつだけ違うのは、fgとgfはいつも同じとは限らないというところですね。
因果と確率を考えることで現実を科学する
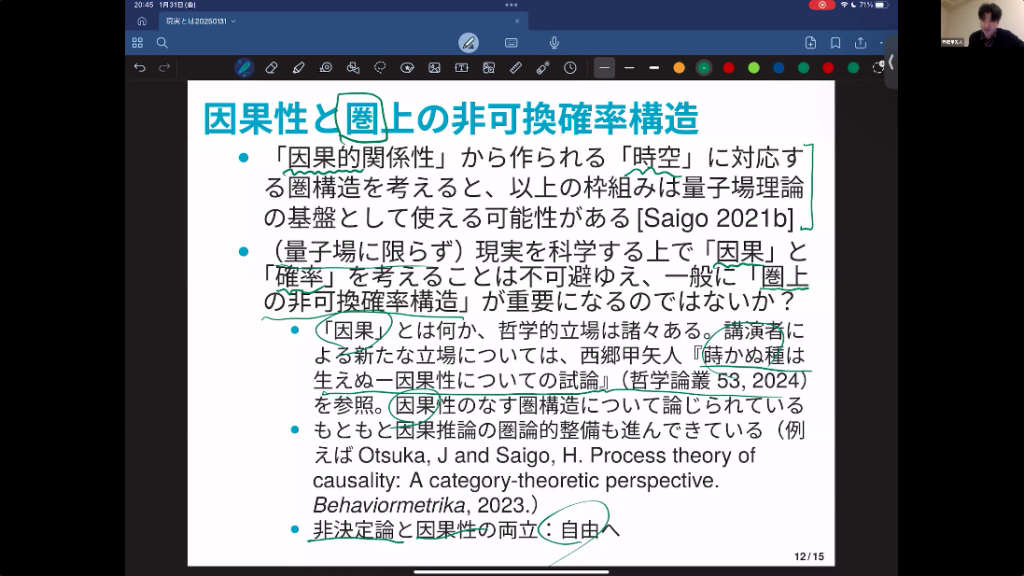
西郷 プロセスの世界について代数を考えると、非可換なものが自然に出てくる。それについて、一つ一つの矢印が確率的に実現したりしなかったりするものがある。そして、先ほどの系と環境の相互関係の中で確率が定まりますという構造を考えると、この非可換確率論といわれるものの枠組みがこの圏から浮かび上がってくるというわけなんですね。
私は量子場に限らず、現実を科学する上でやはり因果と確率を考えることは非常に避け難いのではないかと思います。かなり広い領域で、この圏から定まる非可換確率構造が重要になるのではないかと。
因果というのは、AがあったらBがあるという決定論的なものではなく、AがなければBがないというタイプのものなんです。先ほど、藤井先生も「自由」というキーワードを出されました。私は、自由を考えるためには非決定論と因果性の両方を見なければならないと考えています。
普通に生きている人間にとって、やっぱり未来が全部決まっているなんてことはとても本気では信じられません。量子論を考慮に入れれば、世界全体でそうなっているとは思えないし、万が一そうであったとしても、我々にとってそれが有益な想定とはとても思えません。ですから、決定論じゃないものは必ずどこかのレベルで必要だと思います。
自由を考えるために必要な非決定論と因果性
西郷 一方、何でもありなら自由なのかというと、私は違うと思っています。例えば、解決したい問題がここにあるとします。病気だったり、恋愛だったり、大きくはそれこそ戦争とかジェノサイドとかね。人間の自由って、まさに解決したいと思っている問題を解決できるはずだと考えることです。解決したい問題Aがあって、どんなXからこのAが出てきているのか、つまりXをなくせばAがなくなるような、そういうXを探したい、と考えているはずなんです。
これが、私の言う因果性です。非決定論と、それと矛盾しない因果性。これを両立させることによって、我々は自由という問題を語れるようになるのではないか。この自由を考えるために、数学を拒絶しない形でサイエンスに乗せるには、圏状の非可換確率構造が大事なんじゃないかと、今のところは妄想ですけれども、そんなふうに思っているわけです。
藤井 やっぱり、最後の自由っていうところですよね。世界の構造をいかに理解するかという視点のところで、自由は存在するんだと。決定されていないのでと。そういうところは希望ですよね。世の中の仕組みそのものに自由は常に残されているんだという。
意識もある種の圏上の非可換確率構造ではないか?
藤井 意識の話と西郷先生のお仕事はどうつながるんですか?
西郷 私は意識状態というもの自体を、圏構造からとらえることができるのではないかと思っています。そこにもうひとつ揺らぎの効果を入れてやると、当然その圏状の非可換構造が出てくるはずで、意識状態というのは実は圏代数の上の状態という考え方で理解できるのではないかと。
意識はああも考えるし、こうも走るし、それも同時並行でパラレルに走る。この走り方で、あるパターンが生じると赤と感じるとか、そういうことはありそうな話ではあります。それが圏代数に対応しているかもしれない。ちょうど何かの刺激を与えるのが問いになって、レスポンスみたいな形で出てくるとなると、それが非可換な構造になっていてもおかしくないですし。
藤井 なるほど。じゃあ、意識そのものの仕組みというより、クオリア的な認知の仕組みが非可換確率論的に説明できるよ、という。
西郷 そういうことだと思うんですよね。
藤井 今の話を聞いて考えたら、脳って完全に非可換確率論の世界ですよね。脳のネットワークって書くとノードとノードがつながって、情報がこう処理されて、と言っているけど、それって可換な話をしているようにしか見えないんだよね。
西郷 非自明なリンクがひとつでもあると、圏代数は非可換になる。矢印を本質的に無視できる場合に限り、可換の話になるので。
藤井 だとしたら、脳は全然可換じゃない。
西郷 可換ではないです。意識とかを考える上で、ループってめちゃくちゃ重要じゃないですか。ところが、通常のグラフ理論、ネットワーク理論だと潰しちゃうんですね。だから、そういう複数の経路とかループとかを圧縮して殺したりせずに…
藤井 そのまま生きた状態で計算できるのが圏代数。
西郷 と、私は思っています。
西郷先生にとっての「#現実とは」
藤井 最後に、西郷先生にとっての現実とはなんですか?
西郷 こういうことですね。現実は自由であると。現実について語る時には、結局自由の話になるというのが私の考えです。その意味は、先ほど説明した通りですね。現実を考える時には不定性というのが出てくるし、因果性という問題が出てくる。そのどちらも捨てることができないのが現実であるとすれば、現実の問題って結局自由の問題じゃなか、というふうに思います。
藤井 はい。今日はどうもありがとうございました。
(テキスト:ヨシムラマリ)
本レクチャーのアーカイブはReality Science LabのYouTubeチャンネルにてご視聴いただけます。

